'Tough' 2019 PSLE maths paper: 5 challenging questions over the years
Sign up now: Get tips on how to help your child succeed
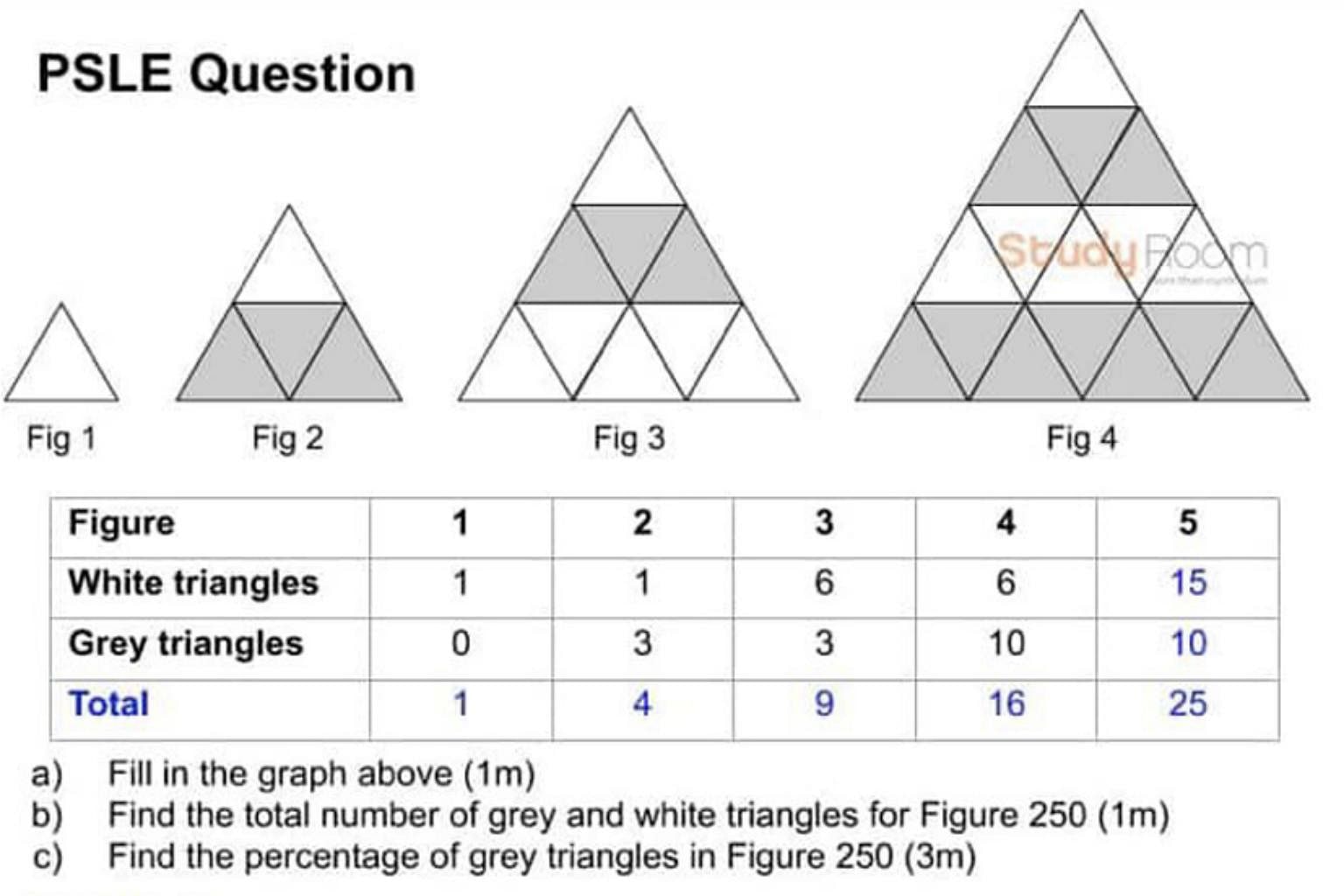
One question in this year's Primary School Leaving Examination mathematics paper asked pupils to figure out patterns in a set of triangles.
PHOTO: COURTESY OF STUDY ROOM/KIASUPARENTS FORUM
Follow topic:
SINGAPORE - A Primary School Leaving Examination (PSLE) mathematics paper last Friday (Sept 27) was said to be so difficult that some pupils who took it were left in tears.
Many parents then took to social media and online forums to voice their concerns about how challenging the paper was.
Discussions over tough PSLE maths questions are an annual affair, with parents taking issue with "tricky" questions from the national examination in 2015 and 2017.
The 2019 paper was said to be among the more challenging papers, with one of its questions brought up repeatedly by tutors.
According to six maths tuition teachers The Straits Times spoke to, the question was harder than many others, but they also noted that there are usually a few difficult PSLE maths questions every year.
And because the difficulty of the maths questions are subjective and depends on the pupils taking the exam, it can be tough to say which questions are definitely the most challenging over the years.
Most of the tutors noted that students struggled particularly with applying concepts they were taught to unique questions they had not encountered before.
These new questions often involved a more cognitive approach, said Mr Wallace Wong, 38, co-founder of Study Room.
"We have noticed a shift in recent years from more standard problem sums which can be drilled, to more creative questions that require thinking and visualisation," said Mr Wong, who has almost 10 years of experience teaching PSLE maths.
Here are some of the tougher PSLE maths questions, by year, according to maths tutors.
1. 2009: Jim bought some chocolates and gave half of them to Ken. Ken bought some sweets and gave half of them to Jim. Jim ate 12 sweets and Ken ate 18 chocolates. The ratio of Jim's sweets to chocolates becomes 1:7 and the ratio of Ken's sweets to chocolates becomes 1:4. How many sweets did Ken buy?
Answer: Ken bought 68 sweets.
Why it was difficult: Mr Zhou Shicai, 35, founder and maths educator at NickleBee Tutors said this question was challenging because it requires more advanced methods to solve. "The efficient approach to solve this question requires simultaneous equations which is a secondary school maths topic," he said. "The pupil could still solve it using the 'Singapore Model Method' or 'Guess and Check' but it would be rather tedious in an exam setting. Nowadays, students are taught the 'Units and Parts' approach to solve this type of questions effectively."
2. 2012: A bakery and a library are 120m apart. They are located between Hong's house and Jeya's house, as shown below. The bakery is exactly half-way between the two houses.
One day, Hong and Jeya started cycling from their houses at the same time and they arrived at the library together. Jeya cycled at 70m per min while Hong cycled at a speed 15m per min faster than Jeya.
a) How much further did Hong cycle than Jeya?
b) How far is Jeya's house from the library?
Answers: a) Hong travelled 240m further than Jeya.
b) Jeya's house is 1,120m from the library.
Why it was difficult: While seemingly straightforward, there was a logical element to the problem which tricked students.
Mr Teo Keng Lik, 43, who has been a tuition teacher teaching primary school maths and science, as well as O and A-level maths, for 18 years, explained that most pupils will think that the difference in the distance travelled is 120m.
But the distance covered by Hong is 120m more than half the distance between the two houses, while the distance covered by Jeya is 120m less than half the distance between the two houses.
This means that the difference in the distance they covered is actually double that of 120m, or 240m.
3. 2013: One machine took 70 minutes while another took 100 minutes to print the same number of copies of a newsletter. The faster machine printed six more copies of the newsletter per minute that the slower one.
a) The slower machine completed the job at 1pm. At what time was the printing started?
b) What was the total number of copies printed by the two machines?
Answers: a) The printer started at 11.20am.
b) The total number of copies printed was 2,800.
Why it was difficult: Mr Teo said that it was a rate question but Primary 6 pupils do not learn the rate concept until secondary school.
"So this question requires pupils to adapt the concept of speed, which they have learnt, to the concept of rate, on their own."
4. 2017: Jess needs 200 pieces of ribbon, each of length 110cm, to decorate a room for a party. Ribbon is sold in rolls of 25m each. What is the least number of rolls of ribbon that Jess needs to buy?
Answer: Jess needs to buy at least 10 rolls.
Why it was difficult: Mr Wong said that the solution is not obvious and requires some creative problem solving.
The ribbon problem requires a pupil to recognise that the unused portion of each roll is discarded.
Once a pupil realises that, the mechanics of solving the problem is straightforward because it simply requires division, so it does not require vigorous maths skills, he said.
5. 2019: This question is based on pupils' recollection of the question in the exam and has not been officially published.
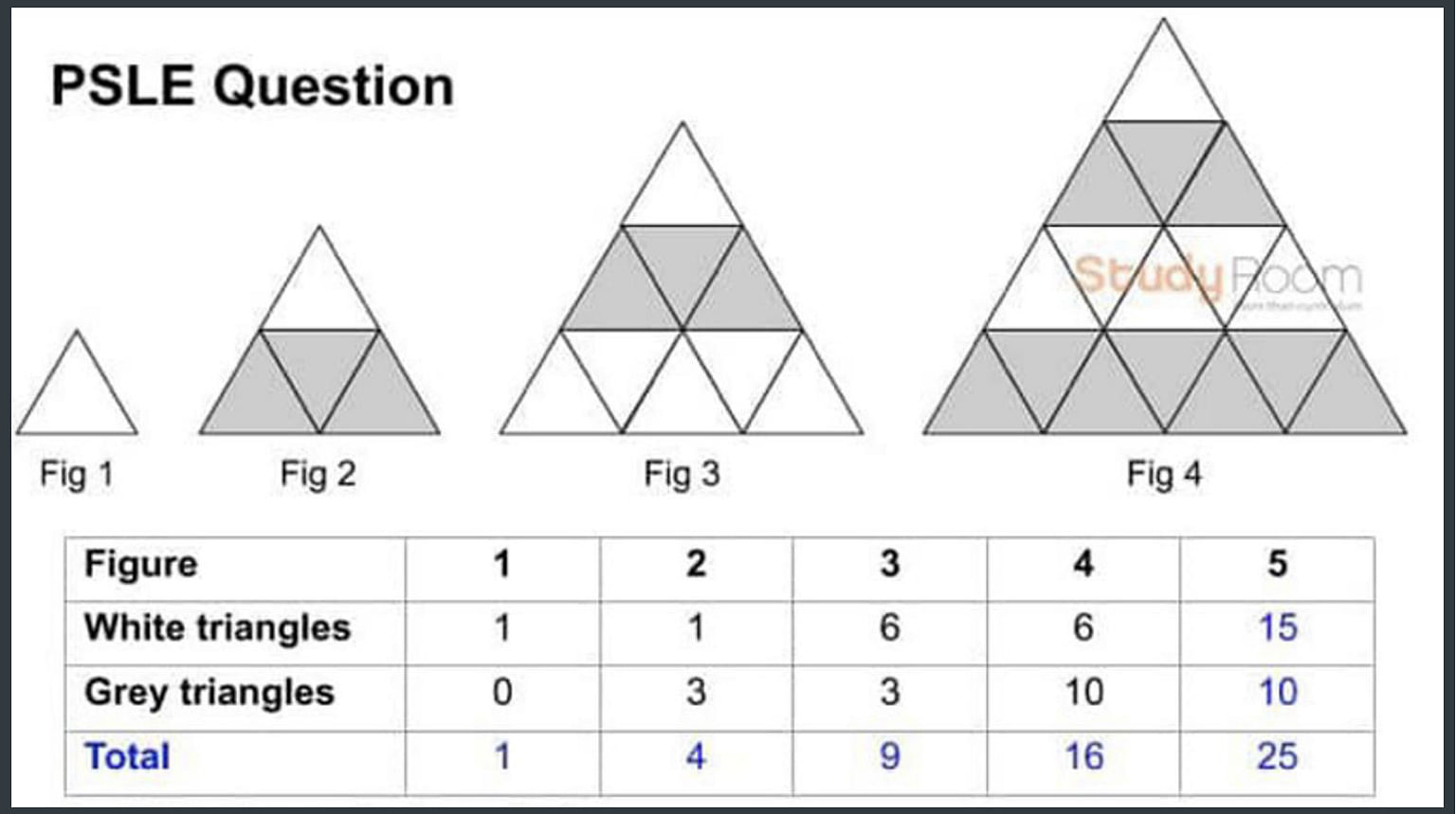
a) Fill in the graph above.
b) Find the total number of grey and white triangles for Figure 250.
c) Find the percentage of grey triangles in Figure 250.
Answers: a) Total number of triangles in Figure 1: 1, Figure 2: 4, Figure 3: 9, Figure 4: 16, Figure 5: 25; white triangles in Figure 5: 15; grey triangles in Figure 5: 10.
b) Figure 250 has 62,500 triangles.
c) The percentage of grey triangles in Figure 250 is 50.2 per cent.
Why it was difficult: Mr Alex Tiew, 32, who has 10 years of tutoring experience, said that typically, for such pattern questions, if a particular row's value is higher than the other, it should be consistent when moving from one figure to another, in ascending order.
But in this question, for the white and grey triangles, their values alternate.
"From memory, I do not recall such situations occurring frequently in past years' PSLE papers," he said, noting that pupils generally find something challenging when they are not exposed to them often.
"Many a time, the materials used by pupils would be past years' PSLE papers and papers from other primary schools. However, there are bound to be new kinds of questions each year, which I think differentiates the A pupils from A* ones."

